最近論理パズルにハマってます
ではさっそく問題をいくつか。

分かりますか?
正解は↓
「水を凍らせて運んだ」
ちょっと簡単すぎるかな。
では次の問題、

これはさっきの問題よりちょっと難しいかも。
正解は↓
「3個の団子が刺さって一串60円の団子。」
2個食べると60円、4個食べると120円、残しても代金は同じですよね。
次の問題、

限られた情報から規則性を導き出す問題。こういうのは大好物です。
では答え↓
「左から、0〜9までの数字のデジタル時計の文字盤の線の数」
イメージしてみれば分かりますね、よって四角の中の数字は「7」
とまあこんな感じの問題を解くのにハマってます。でも、これらが論理パズルと呼べるかって言われると、う〜んと言いたくなる。こういう問題って、応用が効かない上にあんまり論理を使わずに閃き重視みたいな問題が多いですからね。
そんな中で自分がかなり論理パズルに相応しい問題だなと思ったのが次の問題。

答え↓
「あなたは今から私を食べる。」
もしこれが当たって、トラが探検家を食べるのであれば、トラは探検家を見逃さなければならない。もし、トラが探検家を食べないのであれば、探検家の言ったことは外れたのでトラは探検家を食べても良いのだが、それだと探検家の発言は当たることになり矛盾する。つまり、結局トラは探検家を見逃さなければならない。
高校や大学で論理学を学んでいた人はここで「おっ」と何かに気づくのではないだろうか。
そう、これは有名な「自己言及のパラドックス」その他にも、「ワニのパラドックス」などという名で知られている有名な問題。「この文は偽である。」というような文が最も分かりやすい例で、ある命題に自己を含んでしまうことで文が逆説的振る舞いを示し、論理に矛盾が生じてしまい真理値が得られなくなってしまうようなことを、自己言及のパラドックスという。「この文は偽である」が真なら、それは偽だということになり、偽ならばその内容は真ということになり……というように無限に連鎖する。同様に「この文は偽である」が偽なら、それは真ということになり、真ならば内容から偽ということになり……と、この場合も無限に連鎖する。
かの有名なルイス・キャロルは、この自己言及のパラドックスを題材にして、著作「不思議の国のアリス」で、ワニのパラドックスを登場させた。
この「自己言及パラドックス」は、主に大学の論理学で学ぶ。自分も大学の講義でこの内容を聞いた時は、些か混乱した。
そもそも、論理学というのはかなり自分の生活実感とはかけ離れている部分が多い気がする。例えば次のような問題。
Aさん
「何か言ってみてください。もしそれが本当であれば、10ドルさしあげます。もしそれが間違っていることだったら、10ドル以下か10ドル以上のお金をあげます。その場合、ちょうど10ドルさしあげることはできません。」
Bさん
「何か言ってみてください。それが本当のことか間違っていることかに関わらず、あなたに10ドル以上のお金をさしあげます。」
AさんかBさんの、どちらの提案にのるべきだろうか。
大半の人は、Bさんと答えるのではないだろうか。この問題は論理学の基礎ができればそれほど難しくはなく、真理値計算を用いて導けばいい。Aさん、Bさんの提案を表にすると以下のようになる。

Aさんの「ちょうど10ドルあげることはできない」に注目。この条件を見れば、明らかにAさんの提案にのったほうが有利だと分かる。
例えば次のように言ったとしよう。
「あなたは私に、ちょうど10ドルも、ちょうど1000万ドルも、どちらも払わないだろう。」
まずこれが本当のことだと仮定してみる。その場合、Aさんは提案通り、私に10ドルを支払わなければならない。しかし、これは「ちょうど10ドルを払わない」という返答と矛盾する。よって仮定が誤り、この返答は「間違い」になる。すると、これは「どちらも払わないだろう」が間違いであることになるので、「10ドルも1000万ドルもどちらも払わない」の否定になる。つまり「10ドルか1000万ドルかのどちらかを払う」になる。Aさんの提案では、間違いのことを言った場合はAさんはちょうど10ドルを支払うことはできない。よって、Aさんは私に「1000万ドルを払う」しか選択肢がなくなってしまう。
「10ドルを払う」をP、「1000万ドルを払う」をQとおく。すると返答は間違い(=偽)なので、¬P∧¬Qの否定、つまり ¬(¬P∧¬Q) になる。これは何のことはない、P∨Qと同値になる。結果として「Pか、Qかのいずれか」という言い方となり、かつAさん自身の提案でP(=10ドルを払う)の可能性が消去されているので、Q(=1000万ドルを払う)の可能性しか残らない。
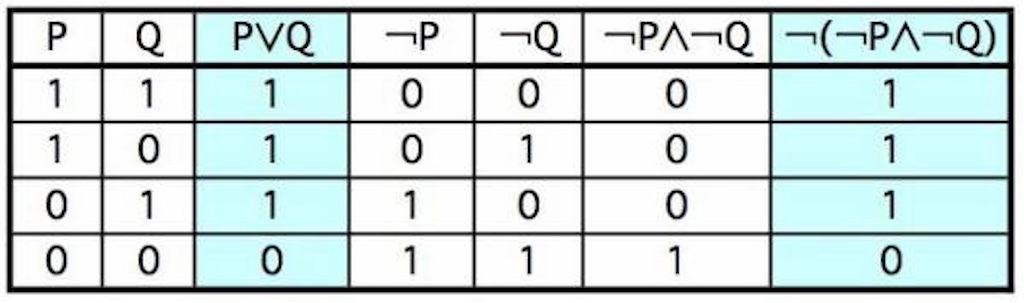
論理学というのは基本的に力技で解かなければならない。断じて閃きではなく、基本的な公式と真理値計算の繰り返しによって答えが導かれる。先程も言ったように、このような公式は、自分の生活実感からかけ離れているものが非常に多い。この問題のように、自分の中での直感と合わないようなものが今でもたくさんある。しかし、それでも言葉や論証を体系的に問うには、特に哲学などにおいては、こういう積み重ねの学問である「論理」が必要になってくる。嫌という程公式や計算を暗記するのが論理学だと言っても過言ではない。そういう「基本の積み重ね」を忘れないようにしなければ、論理的になど一生かかってもなれないだろう。
世の中で「論理的論理的」と騒ぐ連中はこういうのが大嫌いみたいですが。